好了,本篇开始进入正题!内容基本都来自于:Learning to Optimize Tensor Programs. NeurlPS`18
问题定义
上一篇文章讲了 AutoTVM 的大致问题,现在给出数学上面的描述。 首先有一个 \(\mathcal{E}\) 代表所有可能的计算,\(e\in\mathcal{E}\) 就是我们要去优化的计算。对于这个 \(e\) 来说,有一个合法的 schedule space 叫 \(\mathcal{S}_e\),其中每个合法的 schedule 就叫 \(s\in\mathcal{S}_e\)。\(x=g(e,s)\) 是 \(e\) 跟 \(s\) 通过编译器 \(g\) 生成的 low-level code,\(f(x)\) 为这个 \(x\) 在硬件上面实际运行的时间,那么该问题的定义则变成:\[\underset{s\in\mathcal{S}_e}{\operatorname{argmin}}f(g(e,s))\]
这个问题跟现在很多人研究的 hyper-parameter optimization 非常相似,然而 paper 的作者认为,该问题跟传统的 hyper-parameter optimization 有以下几个区别: 第一个区别就是 tensor optimization 比传统的 hyper-parameter optimization 要快很多。因为超参数搜索优化的目标是神经网络的效果,所以训练一次其实是非常慢的,所以超参数搜索可以尝试很多很复杂的方法来进行优化。(比如 GP-UCB 这种,一次 GP kernel regression 要对一个协方差矩阵求逆,实际上是非常慢的,在为什么基于贝叶斯优化的自动调参没有大范围使用?上面有一定的讨论)而 tensor optimization 这个问题,其实你把真的 tensor 程序放到机器上面跑,最慢其实也就几秒。结果你搞了个复杂的方法,要好久才能预测出来结果,那我还不如真的把程序直接放在机器上面跑呢。不过这样的好处是我们可以获得比超参数搜索多得多的数据。 第二个重大的区别是,对于 hyper-parameter optimization 来说,神经网络就是个黑盒子,我们只能根据一些概率的理论去乱调。而对于 tensor optimization 来说,我们有 AST,这是一个非常有力的信息,因为一切运算的秘密其实都隐藏在 AST 里面。 第三个区别是,tensor optimization 的任务之间其实都是相似的,可以进行 transfer learning。 在上一篇文章中我们看到,其实可能去调整的参数还是很多的,这些参数乘起来会变成非常巨大的搜索空间 \(\mathcal{S}_e\)。我们的目的就是在这个巨大的搜索空间中找到最好的 \(s\)。
搜索框架
paper 作者提出的框架是,先搞一个 cost model \(\hat{f}(x)\),然后用这个 \(\hat{f}(x)\) 去指导搜索出 \(s_i\),再把 \((e_i, s_i)\) 放到机器上面跑造出 \(c_i\),然后再去更新 \(\hat{f}(x)\)。
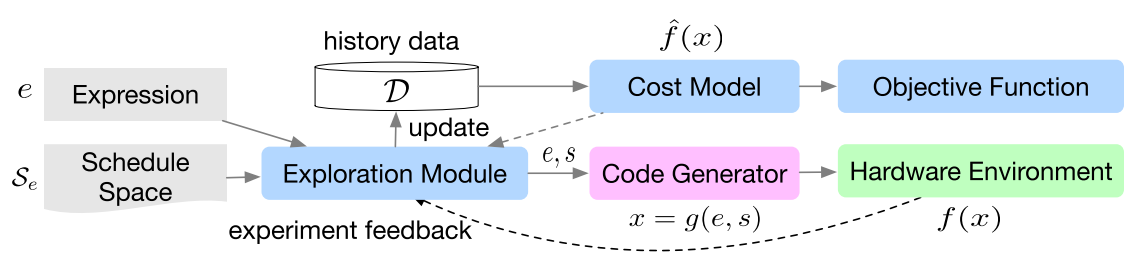
对于这个 cost model,作者搞了两种实现。第一种是陈天奇的传统艺能——XGBoost,第二种是 TreeGRU。(顾名思义,以前的 GRU 或者 LSTM 都是一个输入,这个有多个输入,然后公式小变了一下,其实都大差不差)因为在实际的运用中,TreeGRU 实在是速度有点不行,所以根本都没有 merge 到 master 上面去,在 github 上面版本其实只有 XGBoost。 很显然,这个 cost model 的输出应该是一个预测该程序在硬件上运行的时间。对于最后的 loss,作者也实现了两种方式,第一种是传统的 regression loss:\[\sum_i(\hat{f}(x_i)-c_i)^2\]
第二种则是只考虑他们的相对快慢:\[\sum_{i,j}log(1+e^{-sign(c_i-c_j)(\hat{f}(x_i)-\hat{f}(x_j))})\]
实验表明,两种 loss 效果差不多。 因为这个搜索空间 \(\mathcal{S}_e\) 很大,我们不能枚举整个空间。这里作者使用的方法是,先在 cost model 的指导下通过模拟退火搞出一个候选集,然后再选出来一个相对比较优的集合在硬件上面进行测试,最后更新 cost model。 那么要如何定义一个相对比较优的集合呢?这个集合要同时兼顾 quality 和 diversity。作者给出的最大化式子是这样的:\[L(S)=-\sum_{s\in\mathcal{S}}\hat{f}(g(e,s))+\alpha\sum_{j=1}^m\left|{\cup_{s\in\mathcal{S}}\{s_j\}}\right|\]
这个东西如果不看代码,其实很难知道他到底在干什么东西。看过代码就知道这个 \(s\) 其实已经经过特征抽取,被平铺为一个向量了,然后 \(m\) 就是把这个平铺的向量切成 \(m\) 段。这个式子的意义就是,使得每个子段都尽可能的不一样,并且运行速度还要尽量小。 为什么这个式子要设计成这个样子,看起来不是非常奇怪吗?而且这个式子要怎么优化呢?其实原因就在于如何优化这个式子上面,这个式子是一个 submodular function,可以通过贪心求一个还算凑合的近似解,具体可以看怎么理解次模函数 submodular function? 整个算法的大致过程如下:

贝叶斯优化
对于超参数搜索来说,最广为应用的方式就是贝叶斯优化。那么这个问题能不能套贝叶斯优化呢?在文章中,作者通过 bootstrap 搞出好几个 GBDT,然后通过在多个 GBDT 上面输出的预测值来采取 EI 或者 UCB 等函数,再通过上面的那种过程搜索函数的最值。虽然看起来有些奇怪(GP-UCB 那种其实是可以求出 UCB 的解析解),但总体来说其实还是符合贝叶斯优化的精神的。但是实验效果表明,用不用贝叶斯优化,效果其实都差不太多。
迁移学习
他这个迁移学习模块,我觉得写的其实有点奇怪。后面做的实验也不过是对于不同 size 的卷积进行了迁移学习。然而实际上卷积运算的形式是固定的,cost model 测试的也是同一台机器上面的运算速度,所以其实相当于用的就是同一个 cost model,这个东西本身就是通用的。从这个角度看,把 AST 抽取成一个固定长度的特征就是自然而然的。

对于 XGB 来说,就是简单的抽取 AST 中循环变量所代表的 touched memory 和 outer loop length,在文章中这个叫做 context feature。然而问题在于不同的算子循环变量的数量都有可能是不同的,于是在 transfer learning 中,在代码中使用了一种叫 curve sample 的技术,实际上就是采样 context features 变成一个长度固定的 context relation feature。然而为什么这样就可以提高 transfer learning 的效果,其实我也搞的不太清楚。 在 TreeGRU 中,采取的方式是将循环变量的 context feature 通过 TreeGRU fold 起来,从而得到整个 AST 的 embedding。
实验效果
中间那些不同方式的对比实验就不拿出来贴了,反正最后 state of art 是采用 rank loss 的 XGB。这里贴一个端到端的结果:
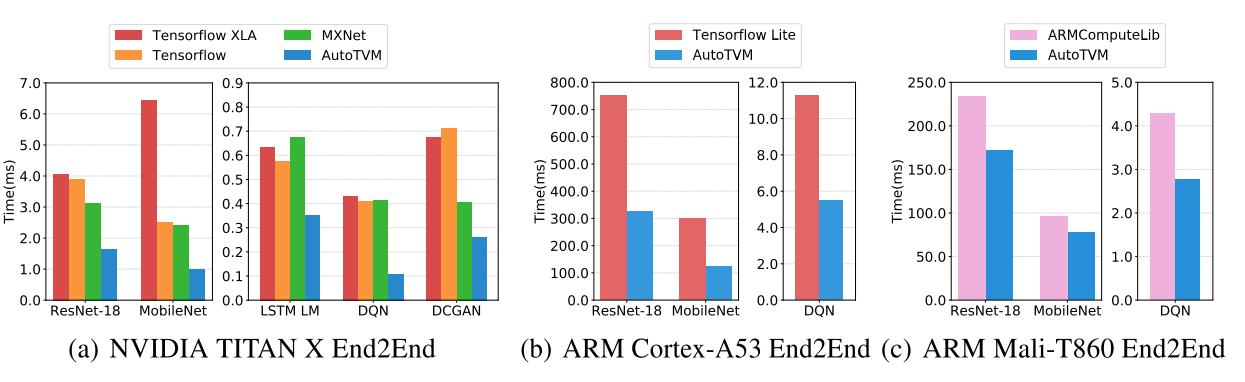
从结果可以看出,优化效果非常强劲,而且越是那种非 benchmark 的网络(如 DQN),优化效果越好。 当然,这个方法并不是完美的,下一篇文章将陈述一些该方法的问题,并讲解几个 AutoTVM 方向最新的文章与成果。