实际上 GNN 在 Source Code 上的应用和创新还有很多。之前的两篇文章都是关于 GNN 建图以及 GNN 跟其他任务相结合的工作，这篇文章就讲一下对 GNN 本身的创新。
Graph Matching Networks for Learning the Similarity of Graph Structured Objects. ICML 2019 就是一个利用 GNN 解决二进制函数相似性问题的工作。这个问题也是 Source Code Modeling 领域的经典问题之一。 二进制函数相似性是一个在信息安全领域应用很广泛的问题。因为很多软件都是不开源的，放在用户电脑上的只能是一些二进制代码。因为编译器、编译选项以及平台的不同，同一个函数的二进制代码也经常是不同的。如果一个函数被检查出了安全漏洞，那这个函数所编译出的所有二进制代码也会有安全漏洞。这些二进制代码放在成千上万用户的电脑上，造成非常大的安全隐患，所以及时找到这些代码是非常重要的。因为二进制代码本身会有一个 Control-flow-graph，所以利用 GNN 解决二进制函数相似性就成为 GNN 的一个应用。
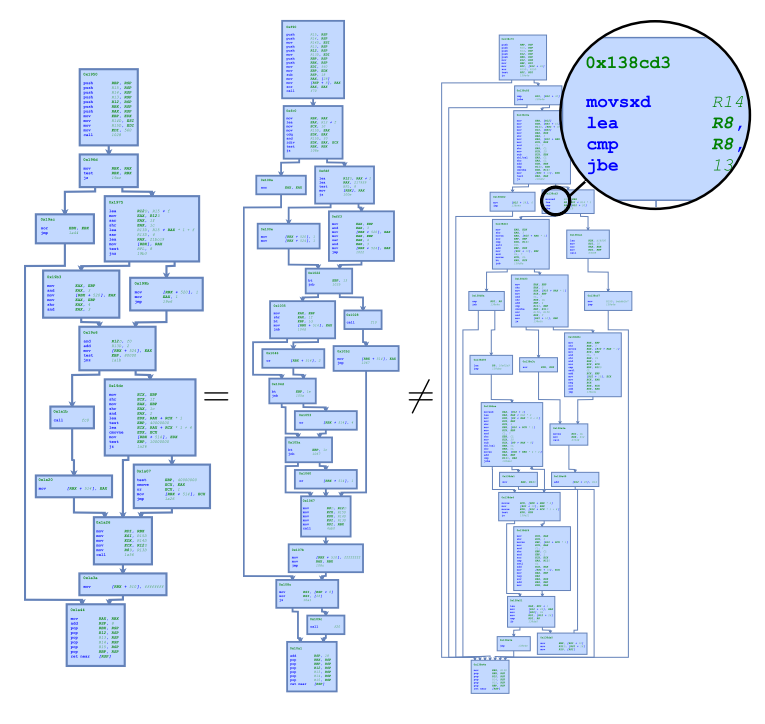
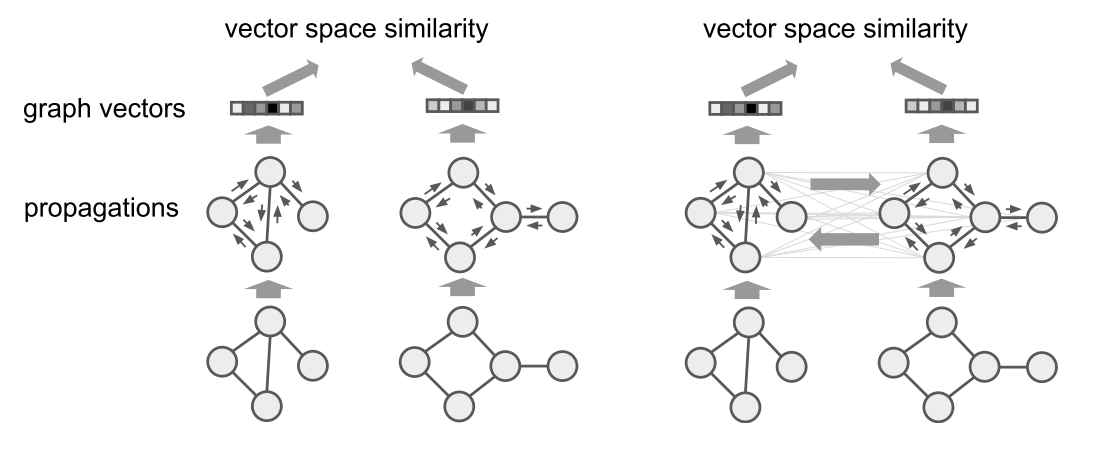
论文中给出两种方式来解决这个问题。第一种是输入一个图输出一个 embedding，通过优化这个 embedding 使得两个相似的图的 embedding 会离得更近。第二种更加直接，输入两个图，输出他们的相似性。这两种方式都是在 GNN 的基础上做的。
第一种方法计算 embedding 的过程没啥好说的，就是输入\((G_1, G_2)\)输出\((h_{G_1},h_{G_2})\)。重点在于最后的 loss 设计，因为跟第二种可以共用相同的 loss，所以放到一起最后讲。 对于第二种方法，大多数步骤跟 GNN 都是一样的。主要区别在于在聚合邻居信息的时候，也要聚合另一张图的信息 \(\mu\)：
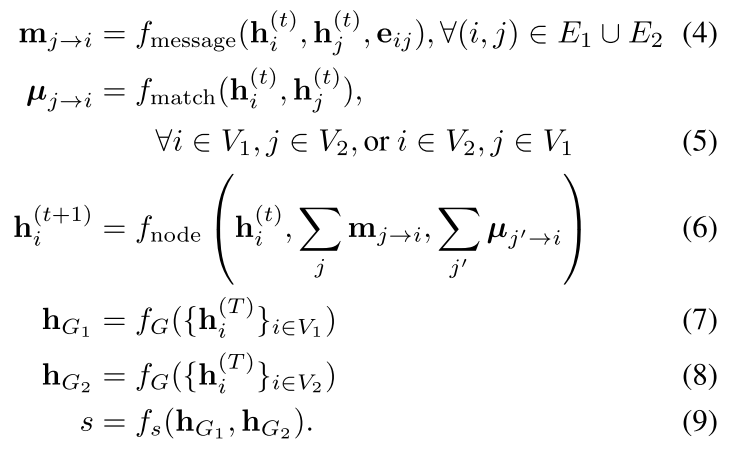
其中\(\mu\)的计算方式如下，上面的\(f_s\)和下面的\(s_h\)都是可以替换的向量相似度计算方式：
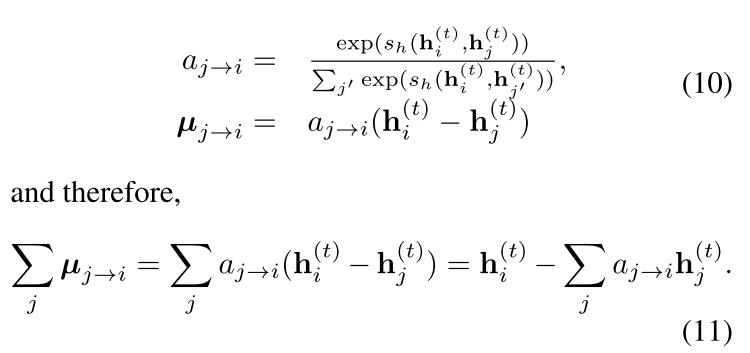
观察公式\((11)\)可以发现，attention 值越大，两个点越相似。所以这个\(\Sigma\mu\)其实就是该点的 embedding 跟另一张图最相似的点的 embedding 的差。如果两个图完全一样，那这个\(\Sigma\mu\)就会一直是\(0\)。所以这个 GMN 的优势就是通过一个图的表示可以更改另一个图的表示，从而捕捉两个图的不相似程度。 下面是两种方法的 loss。论文定义了两种 label，第一种是\((G_1,G_2,t)\)，两个图相似\(t=1\)，不相似\(t=-1\)。第二种是\((G_1,G_2,G_3)\)，其中\(G_1\)跟\(G_2\)更加相似。如果向量相似性用欧拉距离来度量，那可以用一种类似合页 loss 的方式来进行优化：
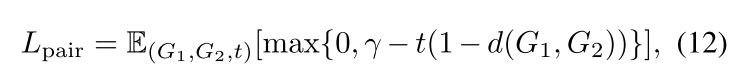
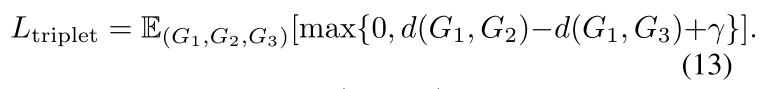
公式\((12)\)可以看做当两个图相似的时候，距离应该小于\(1-\gamma\)，当两个图不相似的时候，距离应该大于\(1+\gamma\)。 公式\((13)\)可以看做\(d(G_1,G_2)\lt d(G_1,G_3)-\gamma\)。
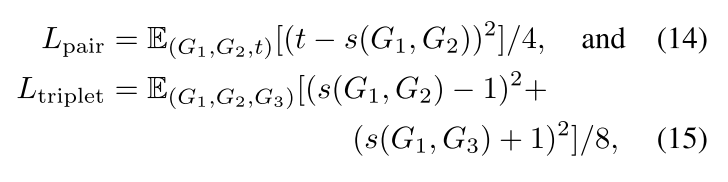也可以按照上面的公式，用 Hamming 相似度来算，这样的好处是向量里面每一维度都是\([1,-1]\)，容易在大型数据库中快速的查询。
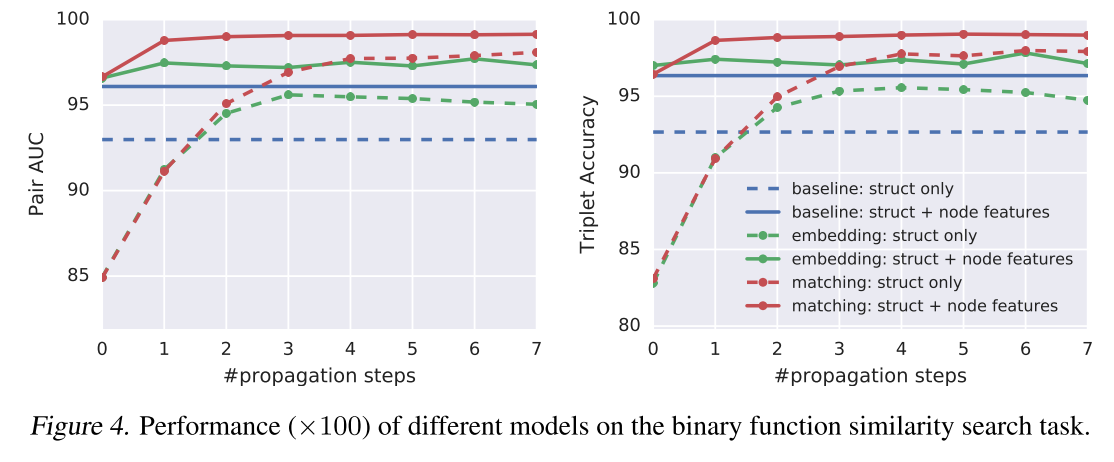
可以看到，效果有一定的提升。这里的 baseline 是 Google 的一个二进制代码查询工具，利用手工构造的图 hash 来寻找相同的代码。